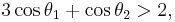Double pendulum
In mathematics, in the area of dynamical systems, a double pendulum is a pendulum with another pendulum attached to its end, and is a simple physical system that exhibits rich dynamic behavior with a strong sensitivity to initial conditions. The motion of a double pendulum is governed by a set of coupled ordinary differential equations. For certain energies its motion is chaotic.
Contents |
Analysis
Several variants of the double pendulum may be considered; the two limbs may be of equal or unequal lengths and masses, they may be simple pendulums or compound pendulums (also called complex pendulums) and the motion may be in three dimensions or restricted to the vertical plane. In the following analysis, the limbs are taken to be identical compound pendulums of length 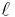 and mass
and mass  , and the motion is restricted to two dimensions.
, and the motion is restricted to two dimensions.
In a compound pendulum, the mass is distributed along its length. If the mass is evenly distributed, then the centre of mass of each limb is at its midpoint, and the limb has a moment of inertia of 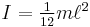 about that point.
about that point.
It is convenient to use the angles between each limb and the vertical as the generalized coordinates defining the configuration of the system. These angles are denoted θ1 and θ2. The position of the centre of mass of each rod may be written in terms of these two coordinates. If the origin of the Cartesian coordinate system is taken to be at the point of suspension of the first pendulum, then the centre of mass of this pendulum is at:
and the centre of mass of the second pendulum is at
This is enough information to write out the Lagrangian.
Lagrangian
The Lagrangian is
The first term is the linear kinetic energy of the center of mass of the bodies and the second term is the rotational kinetic energy around the center of mass of each rod. The last term is the potential energy of the bodies in a uniform gravitational field. The dot-notation indicates the time derivative of the variable in question.
Substituting the coordinates above and rearranging the equation gives
There is only one conserved quantity (the energy), and no conserved momenta. The two momenta may be written as
and
These expressions may be inverted to get
and
The remaining equations of motion are written as
and
These last four equations are explicit formulae for the time evolution of the system given its current state. It is not possible to go further and integrate these equations analytically, to get formulae for θ1 and θ2 as functions of time. It is however possible to perform this integration numerically using the Runge Kutta method or similar techniques.
Chaotic motion
The double pendulum undergoes chaotic motion, and shows a sensitive dependence on initial conditions. The image to the right shows the amount of elapsed time before the pendulum "flips over," as a function of initial conditions. Here, the initial value of θ1 ranges along the x-direction, from −3 to 3. The initial value θ2 ranges along the y-direction, from −3 to 3. The colour of each pixel indicates whether either pendulum flips within 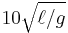 (green), within
(green), within 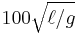 (red),
(red), 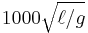 (purple) or
(purple) or 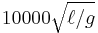 (blue). Initial conditions that don't lead to a flip within
(blue). Initial conditions that don't lead to a flip within 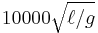 are plotted white.
are plotted white.
The boundary of the central white region is defined in part by energy conservation with the following curve:
Within the region defined by this curve, that is if
then it is energetically impossible for either pendulum to flip. Outside this region, the pendulum can flip, but it is a complex question to determine when it will flip.
The lack of a natural excitation frequency has led to the use of double pendulum systems in seismic resistance designs in buildings, where the building itself is the primary inverted pendulum, and a secondary mass is connected to complete the double pendulum.
See also
References
- Meirovitch, Leonard (1986). Elements of Vibration Analysis (2nd edition ed.). McGraw-Hill Science/Engineering/Math. ISBN 0-07-041342-8.
- Eric W. Weisstein, Double pendulum (2005), ScienceWorld (contains details of the complicated equations involved) and "Double Pendulum" by Rob Morris, Wolfram Demonstrations Project, 2007 (animations of those equations).
- Peter Lynch, Double Pendulum, (2001). (Java applet simulation.)
- Northwestern University, Double Pendulum, (Java applet simulation.)
- Theoretical High-Energy Astrophysics Group at UBC, Double pendulum, (2005).
External links
- Animations and explanations of a double pendulum and a physical double pendulum (two square plates) by Mike Wheatland (Univ. Sydney)
- Video of a double square pendulum with three (almost) identical starting conditions.
- Double pendulum physics simulation from www.myphysicslab.com
- Simulation, equations and explanation of Rott's pendulum
- Comparison videos of a double pendulum with the same initial starting conditions on YouTube
- Double Pendulum Simulator - An open source simulator written in C++ using the Qt tookit.
- Vadas Gintautas, Alfred Hübler (2007). Experimental evidence for mixed reality states in an interreality system Phys. Rev. E 75, 057201 Presents data on an experimental, mixed reality system in which a real and virtual penduluum complexly interact.
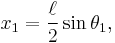
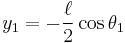
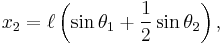
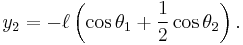
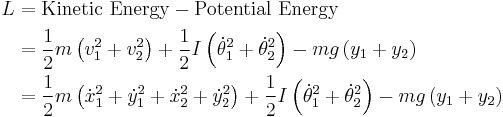
![L = \frac{1}{6} m \ell^2 \left [ {\dot \theta_2}^2 %2B 4 {\dot \theta_1}^2 %2B 3 {\dot \theta_1} {\dot \theta_2} \cos (\theta_1-\theta_2) \right ] %2B \frac{1}{2} m g \ell \left ( 3 \cos \theta_1 %2B \cos \theta_2 \right ).](/2012-wikipedia_en_all_nopic_01_2012/I/818a9a6d0e001cf64b3f05aedd29fe97.png)
![p_{\theta_1} = \frac{\partial L}{\partial {\dot \theta_1}} = \frac{1}{6} m \ell^2 \left [ 8 {\dot \theta_1} %2B 3 {\dot \theta_2} \cos (\theta_1-\theta_2) \right ]](/2012-wikipedia_en_all_nopic_01_2012/I/5d2ce3773944fc8800e86b10d97cdb87.png)
![p_{\theta_2} = \frac{\partial L}{\partial {\dot \theta_2}} = \frac{1}{6} m \ell^2 \left [ 2 {\dot \theta_2} %2B 3 {\dot \theta_1} \cos (\theta_1-\theta_2) \right ].](/2012-wikipedia_en_all_nopic_01_2012/I/6745f6cfa73911f28f6525b38aa1ef63.png)
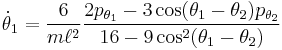
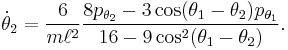
![{\dot p_{\theta_1}} = \frac{\partial L}{\partial \theta_1} = -\frac{1}{2} m \ell^2 \left [ {\dot \theta_1} {\dot \theta_2} \sin (\theta_1-\theta_2) %2B 3 \frac{g}{\ell} \sin \theta_1 \right ]](/2012-wikipedia_en_all_nopic_01_2012/I/df57a7c7102f358e6c77b9a85df778b1.png)
![{\dot p_{\theta_2}} = \frac{\partial L}{\partial \theta_2}
= -\frac{1}{2} m \ell^2 \left [ -{\dot \theta_1} {\dot \theta_2} \sin (\theta_1-\theta_2) %2B \frac{g}{\ell} \sin \theta_2 \right ].](/2012-wikipedia_en_all_nopic_01_2012/I/7f2414e33d60ca9bb057b81e6099a77b.png)